Manipulation des puissances

Les trucs à comprendre

Voilà les principales règles qu’il faut comprendre. Je dis comprendre car idéalement faut savoir pourquoi c’est comme ça. Pas de panique, on va voir qu’on peut en virer pas mal et de toute façon, faut pas hésiter à rayer celles que vous connaissez déjà.

$q^0 = 1$ $q^1 = q$ $q^n = q \cdot q \cdot q \ldots q$ n fois $q^{-n} = \frac{1}{q^n}$ $q^n * q^m = q^{n+m}$ $(q^n)^m = q^{n*m}$ $q^{\frac{1}{2}} = \sqrt{q}$ $q^{\frac{1}{n}} = \sqrt[n]{q}$

Essayons de faire le tri…

On remarque que la ligne 2 est une application de la ligne 3.
De même la ligne 3 c’est la nature même de l’exposant.
On a peut-être pas besoin de les garder dans la liste.
La ligne 1, quant à elle, est une convention qui se démontre si on accepte la ligne 4.

On peut se convaincre que $q^0 = 1$ de cette façon :

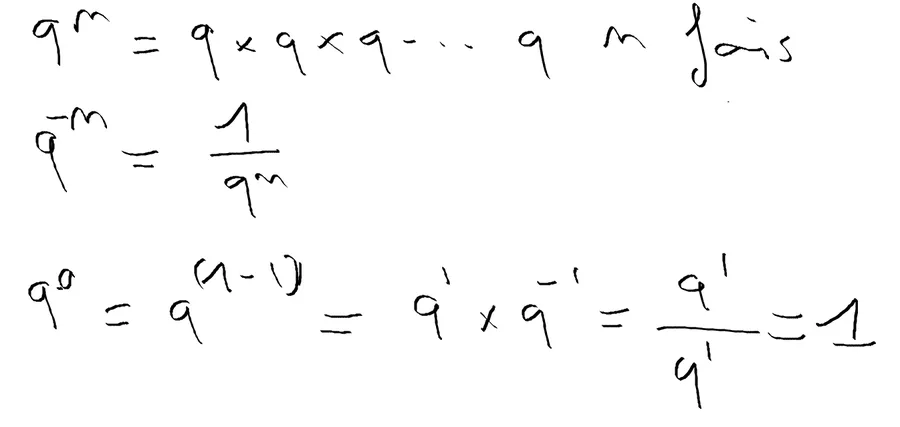
À ce stade il semble utile de ne garder QUE la règle 4 qui peut poser quelques problème de mémorisation.

\[q^{-n} = \frac{1}{q^n}\]

Ceci dit, c’est juste une façon de décrire l’inverse de $q^n$.

Il faut faire un travail similaire sur les autres lignes et ne garder que celles avec lesquelles on est pas à l’aise ou que l’‘on ne connaît pas encore par cœur.

Mise en applications

C’est bien gentil tout ça mais on peut regarder les rappels précédents autant de temps que l’on veut, si on ne les utilise pas on arrivera jamais à se les approprier et à les manipuler efficacement.

Voici des exemples de mise en oeuvre :

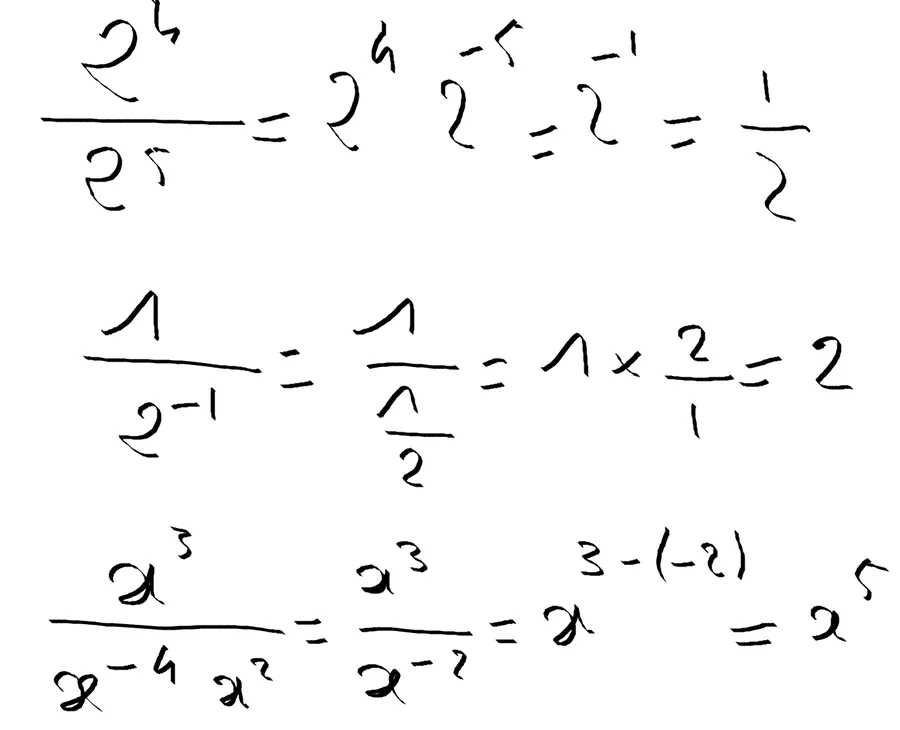
Ligne 1

On utilise la règle 4 pour faire “remonter” le $2^{-5}$.
Bien voir le changement de signe.
On fait ensuite la somme des exposants (règle 5).
À la fin, au lieu d’avoir un exposant négatif, on remet ça sous forme de fraction (règle 4).
Comme $2^{1}$ c’est 2 (règle 2) on simplifie encore l’expression et il reste 1/2.

Ligne 2

Pour le fun j’écris $ 2^{-1}$ sous forme de fraction (règle 4).

Diviser c’est multiplier par son inverse

Je multiplie 1 par l’inverse de 1/2.
Je multiplie donc 1 par 2/1.
Je trouve 2.
On aurait pu directement “faire monter” le $ 2^{-1}$ et trouver 2 en un coup.

Ligne 3

Je fais la somme des puissances au dénominateur (règle 5).
Ensuite on applique la règle 4 et on fait la somme des exposant (règle 5).

Next ?

A toi de jouer.
Personne ne peut le faire à ta place. Prend ton bouquin de maths et fais des exercices, reprends les exercices que vous avez fait en cours
Au pire si tu bute sur un truc, ramène tes calculs sur une copie propre puis demande à ton prof demain